BALL::TVector3< T > Class Template Reference
[Three-dimensional vector.]
#include <BALL/MATHS/vector3.h>
Public Member Functions | |
Constructors and Destructors | |
| TVector3 () | |
| TVector3 (const T *ptr) throw (Exception::NullPointer) | |
| TVector3 (const T &value) | |
| TVector3 (const T &vx, const T &vy, const T &vz) | |
| TVector3 (const TVector3 &vector) | |
| TVector3 (const T &r, const TAngle< T > &phi, const TAngle< T > &theta) | |
| ~TVector3 () | |
| void | clear () |
Arithmetic operators | |
| const TVector3 & | operator+ () const |
| TVector3 | operator- () const |
| TVector3 | operator+ (const TVector3 &b) const |
| TVector3 | operator- (const TVector3 &b) const |
| TVector3 & | operator+= (const TVector3 &vector) |
| TVector3 & | operator-= (const TVector3 &vector) |
| TVector3 | operator* (const T &scalar) const |
| TVector3 & | operator*= (const T &scalar) |
| TVector3 | operator/ (const T &lambda) const throw (Exception::DivisionByZero) |
| TVector3 & | operator/= (const T &lambda) throw (Exception::DivisionByZero) |
| T | operator* (const TVector3 &vector) const |
| TVector3 | operator% (const TVector3 &vector) const |
| TVector3 & | operator%= (const TVector3 &vector) |
Predicates | |
| bool | operator== (const TVector3 &vector) const |
| bool | operator!= (const TVector3 &vector) const |
| bool | operator< (const TVector3 &vector) const |
Needed for MSVC. | |
| bool | isZero () const |
| bool | isOrthogonalTo (const TVector3 &vector) const |
Storable Interface | |
| void | write (PersistenceManager &pm) const |
| bool | read (PersistenceManager &pm) |
Debugging and Diagnostics | |
| void | dump (std::ostream &s=std::cout, Size depth=0) const |
| bool | isValid () const |
Public Attributes | |
Vector components | |
For easier access, the three components of the vector are public members. | |
| T | x |
| T | y |
| T | z |
Private Member Functions | |
| TAngle< T > | getAngle_ (const T &a, const T &b) const |
Assignment | |
| void | set (const T *ptr) throw (Exception::NullPointer) |
| void | set (const T &value) |
| void | set (const T &vx, const T &vy, const T &vz) |
| void | set (const TVector3 &vector) |
| void | set (const T &r, const TAngle< T > &phi, const TAngle< T > &theta) |
| TVector3 & | operator= (const TVector3 &v) |
| TVector3 & | operator= (T value) |
| TVector3 & | operator= (const T *ptr) throw (Exception::NullPointer) |
| void | get (T *ptr) const throw (Exception::NullPointer) |
| void | get (T &x, T &y, T &z) const |
| void | get (TVector3 &vector) const |
| void | get (T &r, TAngle< T > &phi, TAngle< T > &theta) const |
| void | swap (TVector3 &vector) |
| T | getLength () const |
| T | getSquareLength () const |
| TVector3 & | normalize () throw (Exception::DivisionByZero) |
| TVector3 & | negate () |
| T & | operator[] (Position position) throw (Exception::IndexOverflow) |
| const T & | operator[] (Position position) const throw (Exception::IndexOverflow) |
| static const TVector3 & | getZero () |
| static const TVector3 & | getUnit () |
Geometric properties | |
| T | getDistance (const TVector3 &vector) const |
| T | getSquareDistance (const TVector3 &vector) const |
| TAngle< T > | getAngle (const TVector3 &vector) const throw (Exception::DivisionByZero) |
| TVector3 | getOrthogonalProjection (const TVector3 &direction) const |
| static TVector3 | getPerpendicularNormalization (const TVector3 &a, const TVector3 &b, const TVector3 &c) |
| static T | getTripleProduct (const TVector3< T > &a, const TVector3< T > &b, const TVector3< T > &c) |
Detailed Description
template<typename T>
class BALL::TVector3< T >
Generic Three-Dimensional Vector.
Constructor & Destructor Documentation
| BALL_INLINE BALL::TVector3< T >::TVector3 | ( | ) | [inline] |
Default constructor. This method creates a new TVector3 object. The three components are initialized to (T)0.
| BALL_INLINE BALL::TVector3< T >::TVector3 | ( | const T * | ptr | ) | throw (Exception::NullPointer) [inline] |
Array constructor. This constructor creates a TVector3 object from the first three elements pointed to by ptr.
- Parameters:
-
ptr the array to construct from
- Exceptions:
-
NullPointer if ptr == 0
| BALL_INLINE BALL::TVector3< T >::TVector3 | ( | const T & | value | ) | [inline, explicit] |
Scalar constructor. Create a new vector with all components set to the same value.
- Parameters:
-
value the value of all components
| BALL_INLINE BALL::TVector3< T >::TVector3 | ( | const T & | vx, | |
| const T & | vy, | |||
| const T & | vz | |||
| ) | [inline] |
Detailed constructor. Create a new TVector3 object from three variables of type T.
- Parameters:
-
vx assigned to xvy assigned to yvz assigned to z
| BALL_INLINE BALL::TVector3< T >::TVector3 | ( | const TVector3< T > & | vector | ) | [inline] |
| BALL_INLINE BALL::TVector3< T >::TVector3 | ( | const T & | r, | |
| const TAngle< T > & | phi, | |||
| const TAngle< T > & | theta | |||
| ) | [inline] |
Spherical polar coordinate constructor. Create a TVector3 object and set its coordinates to the point described by the three spherical polar coordinates r (radius), phi (azimuth), and theta (co-latitude).
- Parameters:
-
r the radius phi the azimuth theta the co-latitude
| BALL_INLINE BALL::TVector3< T >::~TVector3 | ( | ) | [inline] |
Destructor. Destructs the TVector3 object. As there are no dynamic data structures, nothing happens.
Member Function Documentation
| BALL_INLINE void BALL::TVector3< T >::clear | ( | ) | [inline] |
Clear method The values are set to 0.
References BALL::TVector3< T >::x, BALL::TVector3< T >::y, and BALL::TVector3< T >::z.
| void BALL::TVector3< T >::dump | ( | std::ostream & | s = std::cout, |
|
| Size | depth = 0 | |||
| ) | const [inline] |
Internal state dump. Dump the current internal state of {*this} to the output ostream s with dumping depth depth .
- Parameters:
-
s - output stream where to output the internal state of {*this} depth - the dumping depth
References BALL_DUMP_DEPTH, BALL_DUMP_HEADER, BALL_DUMP_STREAM_PREFIX, BALL_DUMP_STREAM_SUFFIX, BALL::TVector3< T >::x, BALL::TVector3< T >::y, and BALL::TVector3< T >::z.
| BALL_INLINE void BALL::TVector3< T >::get | ( | T & | r, | |
| TAngle< T > & | phi, | |||
| TAngle< T > & | theta | |||
| ) | const [inline] |
Assign to polar coordinates. Sets r, phi, and theta to the coordinates of the vector in spherical polar coordinates.
- Parameters:
-
r the radius (returned) phi the azimuth (returned) theta the co-latitude (returned)
References BALL::TVector3< T >::getAngle_(), BALL::TVector3< T >::x, BALL::TVector3< T >::y, and BALL::TVector3< T >::z.
| void BALL::TVector3< T >::get | ( | TVector3< T > & | vector | ) | const |
Assign to another Vector3. Assigns the vector components to another vector.
- Parameters:
-
vector the vector to be assigned to
| BALL_INLINE void BALL::TVector3< T >::get | ( | T & | x, | |
| T & | y, | |||
| T & | z | |||
| ) | const [inline] |
Assign to three variables of type T.
- Parameters:
-
x the x component y the y component z the z component
References BALL::TVector3< T >::x, BALL::TVector3< T >::y, and BALL::TVector3< T >::z.
| BALL_INLINE void BALL::TVector3< T >::get | ( | T * | ptr | ) | const throw (Exception::NullPointer) [inline] |
Assign to an array. Sets the first three array elements pointed to by ptr to the values of the three vector components.
- Parameters:
-
ptr the array
- Exceptions:
-
NullPointer if ptr == 0
| TAngle<T> BALL::TVector3< T >::getAngle | ( | const TVector3< T > & | vector | ) | const throw (Exception::DivisionByZero) |
Return the enclosed angle of two vectors.
- Exceptions:
-
Exception::DivisionByZero if the product of the squared lengths of the two vectors equals (T)0
Referenced by BALL::GetAngle().
| TAngle<T> BALL::TVector3< T >::getAngle_ | ( | const T & | a, | |
| const T & | b | |||
| ) | const [inline, private] |
Referenced by BALL::TVector3< T >::get().
| T BALL::TVector3< T >::getDistance | ( | const TVector3< T > & | vector | ) | const |
Return the distance to another vector.
| BALL_INLINE T BALL::TVector3< T >::getLength | ( | ) | const [inline] |
Return the length of the vector. The length of the vector is calculated as 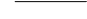 .
.
- Returns:
- T, the vector length
References BALL::TVector3< T >::x, BALL::TVector3< T >::y, and BALL::TVector3< T >::z.
Referenced by BALL::TQuaternion< T >::fromAxisAngle().
| TVector3 BALL::TVector3< T >::getOrthogonalProjection | ( | const TVector3< T > & | direction | ) | const |
Return the orthogonal projection of this vector onto another.
- Parameters:
-
direction the vector to project onto
| static TVector3 BALL::TVector3< T >::getPerpendicularNormalization | ( | const TVector3< T > & | a, | |
| const TVector3< T > & | b, | |||
| const TVector3< T > & | c | |||
| ) | [static] |
Return the perpendicular normalization of the vector
- Parameters:
-
a 1st vector b 2nd vector c 3rd vector
- Returns:
- TVector3 the perpendicular normalization
| T BALL::TVector3< T >::getSquareDistance | ( | const TVector3< T > & | vector | ) | const |
Return the squared distance to another vector.
| BALL_INLINE T BALL::TVector3< T >::getSquareLength | ( | ) | const [inline] |
Return the squared length of the vector. This method avoids the square root needed in getLength, so this method is preferred if possible.
- Returns:
- T,

References BALL::TVector3< T >::x, BALL::TVector3< T >::y, and BALL::TVector3< T >::z.
Referenced by BALL::GetAngle().
| BALL_INLINE T BALL::TVector3< T >::getTripleProduct | ( | const TVector3< T > & | a, | |
| const TVector3< T > & | b, | |||
| const TVector3< T > & | c | |||
| ) | [inline, static] |
Triple product of three vectors. Calculate the parallelepipedal product of three vectors.
- Parameters:
-
a first vector b second vector v third vector
- Returns:
- T the triple product
References BALL::TVector3< T >::x, BALL::TVector3< T >::y, and BALL::TVector3< T >::z.
Referenced by BALL::GetDistance().
| BALL_INLINE const TVector3< T > & BALL::TVector3< T >::getUnit | ( | ) | [inline, static] |
Return a vector with all components 1.
- Returns:
- : TVector4(1, 1, 1, 1)
| BALL_INLINE const TVector3< T > & BALL::TVector3< T >::getZero | ( | ) | [inline, static] |
Return a vector with all components 0.
| bool BALL::TVector3< T >::isOrthogonalTo | ( | const TVector3< T > & | vector | ) | const |
Orthogonality predicate.
| BALL_INLINE bool BALL::TVector3< T >::isValid | ( | ) | const [inline] |
Test if instance is valid. Always returns true.
- Returns:
- bool true
| BALL_INLINE bool BALL::TVector3< T >::isZero | ( | ) | const [inline] |
Zero predicate. The function Maths::isZero is used to compare the values with zero. Maths::isZero
References BALL::Maths::isZero(), BALL::TVector3< T >::x, BALL::TVector3< T >::y, and BALL::TVector3< T >::z.
| BALL_INLINE TVector3< T > & BALL::TVector3< T >::negate | ( | ) | [inline] |
Negate the vector. Negate the three components of the vector
- Returns:
- T, a reference to {*this} vector
References BALL::TVector3< T >::x, BALL::TVector3< T >::y, and BALL::TVector3< T >::z.
| TVector3< T > & BALL::TVector3< T >::normalize | ( | ) | throw (Exception::DivisionByZero) [inline] |
Normalize the vector. The vector is scaled with its length: 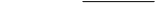 .
.
- Returns:
- T, a reference to the normalized vector
- Exceptions:
-
DivisionByZero if the length of the vector is 0
References BALL::Maths::isZero(), BALL::TVector3< T >::x, BALL::TVector3< T >::y, and BALL::TVector3< T >::z.
Referenced by BALL::TBox3< T >::getDiagonalVector(), BALL::GetIntersection(), and BALL::VIEW::Camera::moveForward().
| bool BALL::TVector3< T >::operator!= | ( | const TVector3< T > & | vector | ) | const |
Inequality operator. The function Maths::isEqual is used to compare the values. Maths::isEqual
- Returns:
- bool, true if the two vectors differ in at least one component, false otherwise
| TVector3 BALL::TVector3< T >::operator% | ( | const TVector3< T > & | vector | ) | const |
Cross product. Return the cross product of this vector and vector.
| TVector3& BALL::TVector3< T >::operator%= | ( | const TVector3< T > & | vector | ) |
Assign to the cross product. Assign the vector to its cross product with another vector.
| T BALL::TVector3< T >::operator* | ( | const TVector3< T > & | vector | ) | const |
Dot product. Return the dot product of this vector and vector.
| BALL_INLINE TVector3< T > BALL::TVector3< T >::operator* | ( | const T & | scalar | ) | const [inline] |
Scalar product. Return TVector3(x * scalar, y * scalar, z * scalar).
- Parameters:
-
scalar,the scalar to multiply by
- Returns:
- TVector3 the scalar product of this vector and
scalar
References BALL::TVector3< T >::x, BALL::TVector3< T >::y, and BALL::TVector3< T >::z.
| BALL_INLINE TVector3< T > & BALL::TVector3< T >::operator*= | ( | const T & | scalar | ) | [inline] |
Multiply by a scalar. Multiply all components of the vector by a scalar value.
- Parameters:
-
scalar the to multiply by
- Returns:
- TVector3&, {*this}
References BALL::TVector3< T >::x, BALL::TVector3< T >::y, and BALL::TVector3< T >::z.
| TVector3 BALL::TVector3< T >::operator+ | ( | const TVector3< T > & | b | ) | const |
| BALL_INLINE const TVector3< T > & BALL::TVector3< T >::operator+ | ( | ) | const [inline] |
Positive sign.
| TVector3& BALL::TVector3< T >::operator+= | ( | const TVector3< T > & | vector | ) |
Add a vector to this vector. Add the components of vector to this vector.
- Parameters:
-
vector the vector to add
- Returns:
- TVector3&, {*this}
| TVector3 BALL::TVector3< T >::operator- | ( | const TVector3< T > & | b | ) | const |
| BALL_INLINE TVector3< T > BALL::TVector3< T >::operator- | ( | ) | const [inline] |
Negative sign.
References BALL::TVector3< T >::x, BALL::TVector3< T >::y, and BALL::TVector3< T >::z.
| TVector3& BALL::TVector3< T >::operator-= | ( | const TVector3< T > & | vector | ) |
Subtract a vector from this vector.
- Parameters:
-
vector the vector to subtract
- Returns:
- TVector3&, {*this}
| TVector3< T > BALL::TVector3< T >::operator/ | ( | const T & | lambda | ) | const throw (Exception::DivisionByZero) [inline] |
Fraction of a vector. Return TVector3(x / lambda, y / lambda, z / lambda).
- Parameters:
-
lambda the scalar value to divide by
- Returns:
- TVector3&
- Exceptions:
-
Exception::DivisionByZero if lambda == (T)0
| TVector3< T > & BALL::TVector3< T >::operator/= | ( | const T & | lambda | ) | throw (Exception::DivisionByZero) [inline] |
Divide a vector by a scalar.
- Parameters:
-
lambda the scalar value to divide by
- Returns:
- TVector3&, {*this}
- Exceptions:
-
Exception::DivisionByZero if lambda == (T)0
| bool BALL::TVector3< T >::operator< | ( | const TVector3< T > & | vector | ) | const |
Needed for MSVC.
| BALL_INLINE TVector3< T > & BALL::TVector3< T >::operator= | ( | const T * | ptr | ) | throw (Exception::NullPointer) [inline] |
Array assignment operator. Assigns the first three elements of an array to the vector components.
- Parameters:
-
ptr the array
- Exceptions:
-
NullPointer if ptr == 0
| BALL_INLINE TVector3< T > & BALL::TVector3< T >::operator= | ( | T | value | ) | [inline] |
Assignment operator. Assign a constant value to all three vector components.
- Parameters:
-
value the constant to assign to x, y, z
References BALL::TVector3< T >::x, BALL::TVector3< T >::y, and BALL::TVector3< T >::z.
| TVector3& BALL::TVector3< T >::operator= | ( | const TVector3< T > & | v | ) |
Assignment operator. Assign the vector components from another vector.
- Parameters:
-
v the vector to assign from
| bool BALL::TVector3< T >::operator== | ( | const TVector3< T > & | vector | ) | const |
Equality operator. The function Maths::isEqual is used to compare the values. Maths::isEqual
- Returns:
- bool, true if all three vector components are equal, false otherwise
| BALL_INLINE const T & BALL::TVector3< T >::operator[] | ( | Position | position | ) | const throw (Exception::IndexOverflow) [inline] |
Constant array-like access to the components.
- Exceptions:
-
Exception::IndexOverflow if index > 2
| BALL_INLINE T & BALL::TVector3< T >::operator[] | ( | Position | position | ) | throw (Exception::IndexOverflow) [inline] |
Mutable array-like access to the components.
- Exceptions:
-
Exception::IndexOverflow if index > 2
| bool BALL::TVector3< T >::read | ( | PersistenceManager & | pm | ) | [inline] |
Persistent stream reading.
References BALL::PersistenceManager::readPrimitive(), BALL::TVector3< T >::x, BALL::TVector3< T >::y, and BALL::TVector3< T >::z.
| BALL_INLINE void BALL::TVector3< T >::set | ( | const T & | r, | |
| const TAngle< T > & | phi, | |||
| const TAngle< T > & | theta | |||
| ) | [inline] |
Assign from spherical polar coordinates. The radius describes the distance of the point from the origin.
phiranges from 0 to ,
, thetaranges from 0 (north pole, positive z-axis) to (south pole, negative z-axis).
(south pole, negative z-axis).
- Coordinates are calculated according to the following formulae:
- Parameters:
-
r the radius phi the azimuth theta the co-latitude
References BALL::TVector3< T >::x, BALL::TVector3< T >::y, and BALL::TVector3< T >::z.
| void BALL::TVector3< T >::set | ( | const TVector3< T > & | vector | ) |
| BALL_INLINE void BALL::TVector3< T >::set | ( | const T & | vx, | |
| const T & | vy, | |||
| const T & | vz | |||
| ) | [inline] |
Assign the vector components.
- Parameters:
-
vx the new x component vy the new y component vz the new z component
References BALL::TVector3< T >::x, BALL::TVector3< T >::y, and BALL::TVector3< T >::z.
| BALL_INLINE void BALL::TVector3< T >::set | ( | const T & | value | ) | [inline] |
Assign from a scalar. Assign value to the three vector components.
- Parameters:
-
value the new value of the components
References BALL::TVector3< T >::x, BALL::TVector3< T >::y, and BALL::TVector3< T >::z.
| BALL_INLINE void BALL::TVector3< T >::set | ( | const T * | ptr | ) | throw (Exception::NullPointer) [inline] |
Assign from an array. Assign the three components x, y, and z from the first three elements of the array pointed to by ptr.
- Parameters:
-
ptr an array
- Exceptions:
-
Nullpointer if ptr == 0
Referenced by BALL::TRegularData3D< ValueType >::clear(), BALL::TSimpleBox3< T >::get(), BALL::HashGrid3< Item >::get(), BALL::TFFT3D< ComplexTraits >::getGridCoordinates(), BALL::GetIntersection(), BALL::operator<<(), and BALL::HashGrid3< Item >::set().
| void BALL::TVector3< T >::swap | ( | TVector3< T > & | vector | ) |
Swap the contents of two vectors.
- Parameters:
-
vector the vector to swap contents with
| void BALL::TVector3< T >::write | ( | PersistenceManager & | pm | ) | const [inline] |
Persistent stream writing.
References BALL::PersistenceManager::writePrimitive(), BALL::TVector3< T >::x, BALL::TVector3< T >::y, and BALL::TVector3< T >::z.
Member Data Documentation
| T BALL::TVector3< T >::x |
x component of the vector
Referenced by BALL::HashGrid3< Item >::calculateMinSpacing(), BALL::TVector3< T >::clear(), BALL::TVector3< T >::dump(), BALL::TQuaternion< T >::fromAxisAngle(), BALL::TVector3< T >::get(), BALL::HashGrid3< Item >::getBox(), BALL::GetDistance(), BALL::TFFT3D< ComplexTraits >::getFourierSpaceMaxX(), BALL::TFFT3D< ComplexTraits >::getFourierSpaceMinX(), BALL::TFFT3D< ComplexTraits >::getGridCoordinates(), BALL::TFFT3D< ComplexTraits >::getInterpolatedValue(), BALL::TVector3< T >::getLength(), BALL::GetPartition(), BALL::TFFT3D< ComplexTraits >::getPhysSpaceMaxX(), BALL::TFFT3D< ComplexTraits >::getPhysSpaceMinX(), BALL::TVector3< T >::getSquareLength(), BALL::TVector3< T >::getTripleProduct(), BALL::TLine3< T >::has(), BALL::TVector3< T >::isZero(), BALL::TRegularData3D< char >::mapInverse_(), BALL::TRegularData3D< char >::mapToCartesian_(), BALL::TVector3< T >::negate(), BALL::TVector3< T >::normalize(), BALL::TVector3< T >::operator*(), BALL::operator*(), BALL::TVector3< T >::operator*=(), BALL::TVector3< T >::operator-(), BALL::TVector3< T >::operator=(), BALL::TFFT3D< ComplexTraits >::operator==(), BALL::operator>>(), BALL::TFFT3D< ComplexTraits >::phase(), BALL::TVector3< T >::read(), BALL::TMatrix4x4< T >::rotate(), BALL::TMatrix4x4< T >::scale(), BALL::TVector3< T >::set(), BALL::TRegularData3D< char >::setDimension(), BALL::TFFT3D< ComplexTraits >::setPhysStepWidth(), BALL::TMatrix4x4< T >::setRotation(), BALL::TMatrix4x4< T >::setScale(), BALL::TMatrix4x4< T >::setTranslation(), BALL::VIEW::GLRenderer::texCoordVector3_(), BALL::TQuaternion< T >::toAxisAngle(), BALL::TMatrix4x4< T >::translate(), BALL::TFFT3D< ComplexTraits >::translate(), and BALL::TVector3< T >::write().
| T BALL::TVector3< T >::y |
y component of the vector
Referenced by BALL::HashGrid3< Item >::calculateMinSpacing(), BALL::TVector3< T >::clear(), BALL::TVector3< T >::dump(), BALL::TQuaternion< T >::fromAxisAngle(), BALL::TVector3< T >::get(), BALL::HashGrid3< Item >::getBox(), BALL::GetDistance(), BALL::TFFT3D< ComplexTraits >::getFourierSpaceMaxY(), BALL::TFFT3D< ComplexTraits >::getFourierSpaceMinY(), BALL::TFFT3D< ComplexTraits >::getGridCoordinates(), BALL::TFFT3D< ComplexTraits >::getInterpolatedValue(), BALL::TVector3< T >::getLength(), BALL::GetPartition(), BALL::TFFT3D< ComplexTraits >::getPhysSpaceMaxY(), BALL::TFFT3D< ComplexTraits >::getPhysSpaceMinY(), BALL::TVector3< T >::getSquareLength(), BALL::TVector3< T >::getTripleProduct(), BALL::TLine3< T >::has(), BALL::TVector3< T >::isZero(), BALL::TRegularData3D< char >::mapInverse_(), BALL::TRegularData3D< char >::mapToCartesian_(), BALL::TVector3< T >::negate(), BALL::TVector3< T >::normalize(), BALL::TVector3< T >::operator*(), BALL::operator*(), BALL::TVector3< T >::operator*=(), BALL::TVector3< T >::operator-(), BALL::TVector3< T >::operator=(), BALL::TFFT3D< ComplexTraits >::operator==(), BALL::operator>>(), BALL::TFFT3D< ComplexTraits >::phase(), BALL::TVector3< T >::read(), BALL::TMatrix4x4< T >::rotate(), BALL::TMatrix4x4< T >::scale(), BALL::TVector3< T >::set(), BALL::TRegularData3D< char >::setDimension(), BALL::TFFT3D< ComplexTraits >::setPhysStepWidth(), BALL::TMatrix4x4< T >::setRotation(), BALL::TMatrix4x4< T >::setScale(), BALL::TMatrix4x4< T >::setTranslation(), BALL::VIEW::GLRenderer::texCoordVector3_(), BALL::TQuaternion< T >::toAxisAngle(), BALL::TMatrix4x4< T >::translate(), BALL::TFFT3D< ComplexTraits >::translate(), and BALL::TVector3< T >::write().
| T BALL::TVector3< T >::z |
z component of the vector
Referenced by BALL::HashGrid3< Item >::calculateMinSpacing(), BALL::TVector3< T >::clear(), BALL::TVector3< T >::dump(), BALL::HashGrid3< Item >::dump(), BALL::TQuaternion< T >::fromAxisAngle(), BALL::TVector3< T >::get(), BALL::HashGrid3< Item >::getBox(), BALL::GetDistance(), BALL::TFFT3D< ComplexTraits >::getFourierSpaceMaxZ(), BALL::TFFT3D< ComplexTraits >::getFourierSpaceMinZ(), BALL::TFFT3D< ComplexTraits >::getGridCoordinates(), BALL::TFFT3D< ComplexTraits >::getInterpolatedValue(), BALL::TVector3< T >::getLength(), BALL::GetPartition(), BALL::TFFT3D< ComplexTraits >::getPhysSpaceMaxZ(), BALL::TFFT3D< ComplexTraits >::getPhysSpaceMinZ(), BALL::TVector3< T >::getSquareLength(), BALL::TVector3< T >::getTripleProduct(), BALL::TLine3< T >::has(), BALL::TVector3< T >::isZero(), BALL::TRegularData3D< char >::mapInverse_(), BALL::TRegularData3D< char >::mapToCartesian_(), BALL::TVector3< T >::negate(), BALL::TVector3< T >::normalize(), BALL::TVector3< T >::operator*(), BALL::operator*(), BALL::TVector3< T >::operator*=(), BALL::TVector3< T >::operator-(), BALL::TVector3< T >::operator=(), BALL::TFFT3D< ComplexTraits >::operator==(), BALL::operator>>(), BALL::TFFT3D< ComplexTraits >::phase(), BALL::TVector3< T >::read(), BALL::TMatrix4x4< T >::rotate(), BALL::TMatrix4x4< T >::scale(), BALL::TVector3< T >::set(), BALL::TRegularData3D< char >::setDimension(), BALL::TFFT3D< ComplexTraits >::setPhysStepWidth(), BALL::TMatrix4x4< T >::setRotation(), BALL::TMatrix4x4< T >::setScale(), BALL::TMatrix4x4< T >::setTranslation(), BALL::VIEW::GLRenderer::texCoordVector3_(), BALL::TQuaternion< T >::toAxisAngle(), BALL::TMatrix4x4< T >::translate(), BALL::TFFT3D< ComplexTraits >::translate(), and BALL::TVector3< T >::write().
![\[ x = r \sin \theta \cos \phi \]](form_41.png)
![\[ y = r \sin \theta \sin \phi \]](form_42.png)
![\[ z = r \cos \theta \]](form_43.png)